Working with Multidimensional Coordinates¶
Author: Ryan Abernathey
Many datasets have physical coordinates which differ from their logical coordinates. Xarray provides several ways to plot and analyze such datasets.
%matplotlib inline
import numpy as np
import pandas as pd
import xarray as xr
import cartopy.crs as ccrs
from matplotlib import pyplot as plt
print("numpy version : ", np.__version__)
print("pandas version : ", pd.__version__)
print("xarray version : ", xr.version.version)
('numpy version : ', '1.11.0')
('pandas version : ', u'0.18.0')
('xarray version : ', '0.7.2-32-gf957eb8')
As an example, consider this dataset from the xarray-data repository.
! curl -L -O https://github.com/pydata/xarray-data/raw/master/RASM_example_data.nc
ds = xr.open_dataset('RASM_example_data.nc')
ds
<xarray.Dataset>
Dimensions: (time: 36, x: 275, y: 205)
Coordinates:
* time (time) datetime64[ns] 1980-09-16T12:00:00 1980-10-17 ...
yc (y, x) float64 16.53 16.78 17.02 17.27 17.51 17.76 18.0 18.25 ...
xc (y, x) float64 189.2 189.4 189.6 189.7 189.9 190.1 190.2 190.4 ...
* x (x) int64 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 ...
* y (y) int64 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 ...
Data variables:
Tair (time, y, x) float64 nan nan nan nan nan nan nan nan nan nan ...
Attributes:
title: /workspace/jhamman/processed/R1002RBRxaaa01a/lnd/temp/R1002RBRxaaa01a.vic.ha.1979-09-01.nc
institution: U.W.
source: RACM R1002RBRxaaa01a
output_frequency: daily
output_mode: averaged
convention: CF-1.4
references: Based on the initial model of Liang et al., 1994, JGR, 99, 14,415- 14,429.
comment: Output from the Variable Infiltration Capacity (VIC) model.
nco_openmp_thread_number: 1
NCO: 4.3.7
history: history deleted for brevity
In this example, the logical coordinates are x and y, while
the physical coordinates are xc and yc, which represent the
latitudes and longitude of the data.
print(ds.xc.attrs)
print(ds.yc.attrs)
OrderedDict([(u'long_name', u'longitude of grid cell center'), (u'units', u'degrees_east'), (u'bounds', u'xv')])
OrderedDict([(u'long_name', u'latitude of grid cell center'), (u'units', u'degrees_north'), (u'bounds', u'yv')])
Plotting¶
Let’s examine these coordinate variables by plotting them.
fig, (ax1, ax2) = plt.subplots(ncols=2, figsize=(14,4))
ds.xc.plot(ax=ax1)
ds.yc.plot(ax=ax2)
<matplotlib.collections.QuadMesh at 0x118688fd0>
/Users/rpa/anaconda/lib/python2.7/site-packages/matplotlib/collections.py:590: FutureWarning: elementwise comparison failed; returning scalar instead, but in the future will perform elementwise comparison
if self._edgecolors == str('face'):
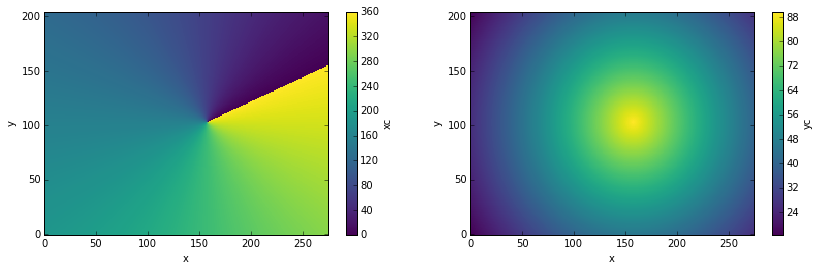
Note that the variables xc (longitude) and yc (latitude) are
two-dimensional scalar fields.
If we try to plot the data variable Tair, by default we get the
logical coordinates.
ds.Tair[0].plot()
<matplotlib.collections.QuadMesh at 0x11b6da890>
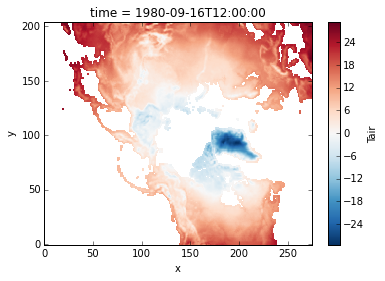
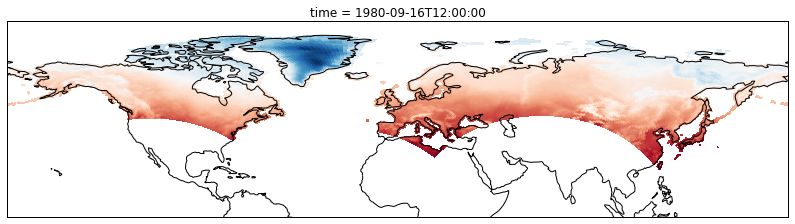
In order to visualize the data on a conventional latitude-longitude grid, we can take advantage of xarray’s ability to apply cartopy map projections.
plt.figure(figsize=(14,6))
ax = plt.axes(projection=ccrs.PlateCarree())
ax.set_global()
ds.Tair[0].plot.pcolormesh(ax=ax, transform=ccrs.PlateCarree(), x='xc', y='yc', add_colorbar=False)
ax.coastlines()
ax.set_ylim([0,90]);
Multidimensional Groupby¶
The above example allowed us to visualize the data on a regular
latitude-longitude grid. But what if we want to do a calculation that
involves grouping over one of these physical coordinates (rather than
the logical coordinates), for example, calculating the mean temperature
at each latitude. This can be achieved using xarray’s groupby
function, which accepts multidimensional variables. By default,
groupby will use every unique value in the variable, which is
probably not what we want. Instead, we can use the groupby_bins
function to specify the output coordinates of the group.
# define two-degree wide latitude bins
lat_bins = np.arange(0,91,2)
# define a label for each bin corresponding to the central latitude
lat_center = np.arange(1,90,2)
# group according to those bins and take the mean
Tair_lat_mean = ds.Tair.groupby_bins('xc', lat_bins, labels=lat_center).mean()
# plot the result
Tair_lat_mean.plot()
[<matplotlib.lines.Line2D at 0x11cb92e90>]
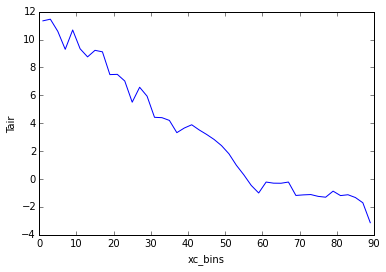
Note that the resulting coordinate for the groupby_bins operation
got the _bins suffix appended: xc_bins. This help us distinguish
it from the original multidimensional variable xc.