Calculating Seasonal Averages from Timeseries of Monthly Means¶
Author: Joe Hamman
The data used for this example can be found in the xarray-data repository.
Suppose we have a netCDF or xarray Dataset of monthly mean data and we want to calculate the seasonal average. To do this properly, we need to calculate the weighted average considering that each month has a different number of days.
Suppose we have a netCDF or xarray.Dataset of monthly mean data and
we want to calculate the seasonal average. To do this properly, we need
to calculate the weighted average considering that each month has a
different number of days.
%matplotlib inline
import numpy as np
import pandas as pd
import xarray as xr
from netCDF4 import num2date
import matplotlib.pyplot as plt
print("numpy version : ", np.__version__)
print("pandas version : ", pd.__version__)
print("xarray version : ", xr.__version__)
numpy version : 1.11.1
pandas version : 0.18.1
xarray version : 0.8.2
Some calendar information so we can support any netCDF calendar.¶
dpm = {'noleap': [0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31],
'365_day': [0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31],
'standard': [0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31],
'gregorian': [0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31],
'proleptic_gregorian': [0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31],
'all_leap': [0, 31, 29, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31],
'366_day': [0, 31, 29, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31],
'360_day': [0, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30]}
A few calendar functions to determine the number of days in each month¶
If you were just using the standard calendar, it would be easy to use
the calendar.month_range function.
def leap_year(year, calendar='standard'):
"""Determine if year is a leap year"""
leap = False
if ((calendar in ['standard', 'gregorian',
'proleptic_gregorian', 'julian']) and
(year % 4 == 0)):
leap = True
if ((calendar == 'proleptic_gregorian') and
(year % 100 == 0) and
(year % 400 != 0)):
leap = False
elif ((calendar in ['standard', 'gregorian']) and
(year % 100 == 0) and (year % 400 != 0) and
(year < 1583)):
leap = False
return leap
def get_dpm(time, calendar='standard'):
"""
return a array of days per month corresponding to the months provided in `months`
"""
month_length = np.zeros(len(time), dtype=np.int)
cal_days = dpm[calendar]
for i, (month, year) in enumerate(zip(time.month, time.year)):
month_length[i] = cal_days[month]
if leap_year(year, calendar=calendar):
month_length[i] += 1
return month_length
Open the Dataset¶
ds = xr.tutorial.load_dataset('rasm')
print(ds)
<xarray.Dataset>
Dimensions: (time: 36, x: 275, y: 205)
Coordinates:
* time (time) datetime64[ns] 1980-09-16T12:00:00 1980-10-17 ...
* y (y) int64 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 ...
* x (x) int64 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 ...
Data variables:
Tair (time, y, x) float64 nan nan nan nan nan nan nan nan nan nan ...
yc (y, x) float64 16.53 16.78 17.02 17.27 17.51 17.76 18.0 18.25 ...
xc (y, x) float64 189.2 189.4 189.6 189.7 189.9 190.1 190.2 190.4 ...
Attributes:
title: /workspace/jhamman/processed/R1002RBRxaaa01a/lnd/temp/R1002RBRxaaa01a.vic.ha.1979-09-01.nc
institution: U.W.
source: RACM R1002RBRxaaa01a
output_frequency: daily
output_mode: averaged
convention: CF-1.4
references: Based on the initial model of Liang et al., 1994, JGR, 99, 14,415- 14,429.
comment: Output from the Variable Infiltration Capacity (VIC) model.
nco_openmp_thread_number: 1
NCO: 4.3.7
history: history deleted for brevity
Now for the heavy lifting:¶
We first have to come up with the weights, - calculate the month lengths
for each monthly data record - calculate weights using
groupby('time.season')
Finally, we just need to multiply our weights by the Dataset and sum
allong the time dimension.
# Make a DataArray with the number of days in each month, size = len(time)
month_length = xr.DataArray(get_dpm(ds.time.to_index(), calendar='noleap'),
coords=[ds.time], name='month_length')
# Calculate the weights by grouping by 'time.season'.
# Conversion to float type ('astype(float)') only necessary for Python 2.x
weights = month_length.groupby('time.season') / month_length.astype(float).groupby('time.season').sum()
# Test that the sum of the weights for each season is 1.0
np.testing.assert_allclose(weights.groupby('time.season').sum().values, np.ones(4))
# Calculate the weighted average
ds_weighted = (ds * weights).groupby('time.season').sum(dim='time')
print(ds_weighted)
<xarray.Dataset>
Dimensions: (season: 4, x: 275, y: 205)
Coordinates:
* y (y) int64 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 ...
* x (x) int64 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 ...
* season (season) object 'DJF' 'JJA' 'MAM' 'SON'
Data variables:
Tair (season, y, x) float64 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 ...
xc (season, y, x) float64 189.2 189.4 189.6 189.7 189.9 190.1 ...
yc (season, y, x) float64 16.53 16.78 17.02 17.27 17.51 17.76 18.0 ...
# only used for comparisons
ds_unweighted = ds.groupby('time.season').mean('time')
ds_diff = ds_weighted - ds_unweighted
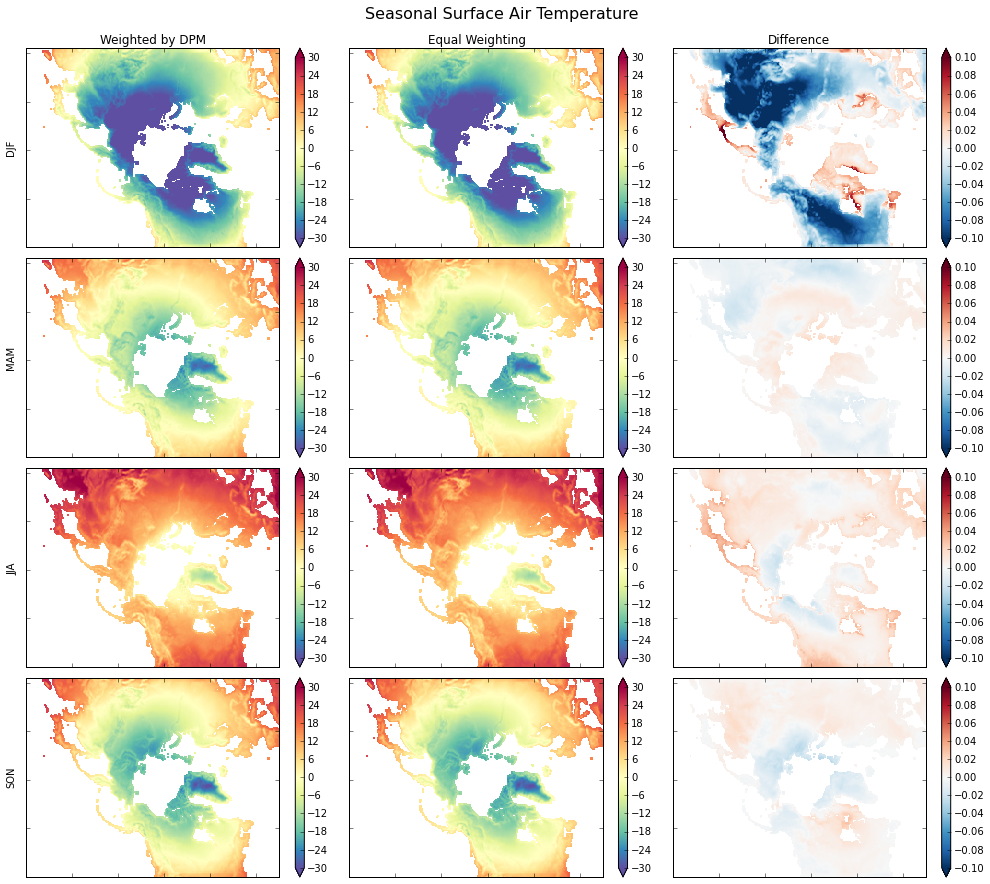
# Quick plot to show the results
notnull = pd.notnull(ds_unweighted['Tair'][0])
fig, axes = plt.subplots(nrows=4, ncols=3, figsize=(14,12))
for i, season in enumerate(('DJF', 'MAM', 'JJA', 'SON')):
ds_weighted['Tair'].sel(season=season).where(notnull).plot.pcolormesh(
ax=axes[i, 0], vmin=-30, vmax=30, cmap='Spectral_r',
add_colorbar=True, extend='both')
ds_unweighted['Tair'].sel(season=season).where(notnull).plot.pcolormesh(
ax=axes[i, 1], vmin=-30, vmax=30, cmap='Spectral_r',
add_colorbar=True, extend='both')
ds_diff['Tair'].sel(season=season).where(notnull).plot.pcolormesh(
ax=axes[i, 2], vmin=-0.1, vmax=.1, cmap='RdBu_r',
add_colorbar=True, extend='both')
axes[i, 0].set_ylabel(season)
axes[i, 1].set_ylabel('')
axes[i, 2].set_ylabel('')
for ax in axes.flat:
ax.axes.get_xaxis().set_ticklabels([])
ax.axes.get_yaxis().set_ticklabels([])
ax.axes.axis('tight')
ax.set_xlabel('')
axes[0, 0].set_title('Weighted by DPM')
axes[0, 1].set_title('Equal Weighting')
axes[0, 2].set_title('Difference')
plt.tight_layout()
fig.suptitle('Seasonal Surface Air Temperature', fontsize=16, y=1.02)
<matplotlib.text.Text at 0x117c18048>
# Wrap it into a simple function
def season_mean(ds, calendar='standard'):
# Make a DataArray of season/year groups
year_season = xr.DataArray(ds.time.to_index().to_period(freq='Q-NOV').to_timestamp(how='E'),
coords=[ds.time], name='year_season')
# Make a DataArray with the number of days in each month, size = len(time)
month_length = xr.DataArray(get_dpm(ds.time.to_index(), calendar=calendar),
coords=[ds.time], name='month_length')
# Calculate the weights by grouping by 'time.season'
weights = month_length.groupby('time.season') / month_length.groupby('time.season').sum()
# Test that the sum of the weights for each season is 1.0
np.testing.assert_allclose(weights.groupby('time.season').sum().values, np.ones(4))
# Calculate the weighted average
return (ds * weights).groupby('time.season').sum(dim='time')