Interpolating data¶
xarray offers flexible interpolation routines, which have a similar interface to our indexing.
Note
interp requires scipy installed.
Scalar and 1-dimensional interpolation¶
Interpolating a DataArray works mostly like labeled
indexing of a DataArray,
In [1]: da = xr.DataArray(np.sin(0.3 * np.arange(12).reshape(4, 3)),
...: [('time', np.arange(4)),
...: ('space', [0.1, 0.2, 0.3])])
...:
# label lookup
In [2]: da.sel(time=3)
Out[2]:
<xarray.DataArray (space: 3)>
array([ 0.42738 , 0.14112 , -0.157746])
Coordinates:
time int64 3
* space (space) float64 0.1 0.2 0.3
# interpolation
In [3]: da.interp(time=2.5)
�����������������������������������������������������������������������������������������������������������������������������������������������������������Out[3]:
<xarray.DataArray (space: 3)>
array([0.700614, 0.502165, 0.258859])
Coordinates:
* space (space) float64 0.1 0.2 0.3
time float64 2.5
Similar to the indexing, interp() also accepts an
array-like, which gives the interpolated result as an array.
# label lookup
In [4]: da.sel(time=[2, 3])
Out[4]:
<xarray.DataArray (time: 2, space: 3)>
array([[ 0.973848, 0.863209, 0.675463],
[ 0.42738 , 0.14112 , -0.157746]])
Coordinates:
* time (time) int64 2 3
* space (space) float64 0.1 0.2 0.3
# interpolation
In [5]: da.interp(time=[2.5, 3.5])
�������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������Out[5]:
<xarray.DataArray (time: 2, space: 3)>
array([[0.700614, 0.502165, 0.258859],
[ nan, nan, nan]])
Coordinates:
* space (space) float64 0.1 0.2 0.3
* time (time) float64 2.5 3.5
To interpolate data with a numpy.datetime64() coordinate you can pass a string.
In [6]: da_dt64 = xr.DataArray([1, 3],
...: [('time', pd.date_range('1/1/2000', '1/3/2000', periods=2))])
...:
In [7]: da_dt64.interp(time='2000-01-02')
Out[7]:
<xarray.DataArray ()>
array(2.)
Coordinates:
time datetime64[ns] 2000-01-02
The interpolated data can be merged into the original DataArray
by specifying the time periods required.
In [8]: da_dt64.interp(time=pd.date_range('1/1/2000', '1/3/2000', periods=3))
Out[8]:
<xarray.DataArray (time: 3)>
array([1., 2., 3.])
Coordinates:
* time (time) datetime64[ns] 2000-01-01 2000-01-02 2000-01-03
Interpolation of data indexed by a CFTimeIndex is also
allowed. See Non-standard calendars and dates outside the Timestamp-valid range for examples.
Note
Currently, our interpolation only works for regular grids.
Therefore, similarly to sel(),
only 1D coordinates along a dimension can be used as the
original coordinate to be interpolated.
Multi-dimensional Interpolation¶
Like sel(), interp()
accepts multiple coordinates. In this case, multidimensional interpolation
is carried out.
# label lookup
In [9]: da.sel(time=2, space=0.1)
Out[9]:
<xarray.DataArray ()>
array(0.973848)
Coordinates:
time int64 2
space float64 0.1
# interpolation
In [10]: da.interp(time=2.5, space=0.15)
����������������������������������������������������������������������������������������������������������Out[10]:
<xarray.DataArray ()>
array(0.601389)
Coordinates:
time float64 2.5
space float64 0.15
Array-like coordinates are also accepted:
# label lookup
In [11]: da.sel(time=[2, 3], space=[0.1, 0.2])
Out[11]:
<xarray.DataArray (time: 2, space: 2)>
array([[0.973848, 0.863209],
[0.42738 , 0.14112 ]])
Coordinates:
* time (time) int64 2 3
* space (space) float64 0.1 0.2
# interpolation
In [12]: da.interp(time=[1.5, 2.5], space=[0.15, 0.25])
��������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������Out[12]:
<xarray.DataArray (time: 2, space: 2)>
array([[0.888106, 0.867052],
[0.601389, 0.380512]])
Coordinates:
* time (time) float64 1.5 2.5
* space (space) float64 0.15 0.25
interp_like() method is a useful shortcut. This
method interpolates an xarray object onto the coordinates of another xarray
object. For example, if we want to compute the difference between
two DataArray s (da and other) staying on slightly
different coordinates,
In [13]: other = xr.DataArray(np.sin(0.4 * np.arange(9).reshape(3, 3)),
....: [('time', [0.9, 1.9, 2.9]),
....: ('space', [0.15, 0.25, 0.35])])
....:
it might be a good idea to first interpolate da so that it will stay on the
same coordinates of other, and then subtract it.
interp_like() can be used for such a case,
# interpolate da along other's coordinates
In [14]: interpolated = da.interp_like(other)
In [15]: interpolated
Out[15]:
<xarray.DataArray (time: 3, space: 3)>
array([[0.786691, 0.911298, nan],
[0.912444, 0.788879, nan],
[0.347678, 0.069452, nan]])
Coordinates:
* time (time) float64 0.9 1.9 2.9
* space (space) float64 0.15 0.25 0.35
It is now possible to safely compute the difference other - interpolated.
Interpolation methods¶
We use scipy.interpolate.interp1d() for 1-dimensional interpolation and
scipy.interpolate.interpn() for multi-dimensional interpolation.
The interpolation method can be specified by the optional method argument.
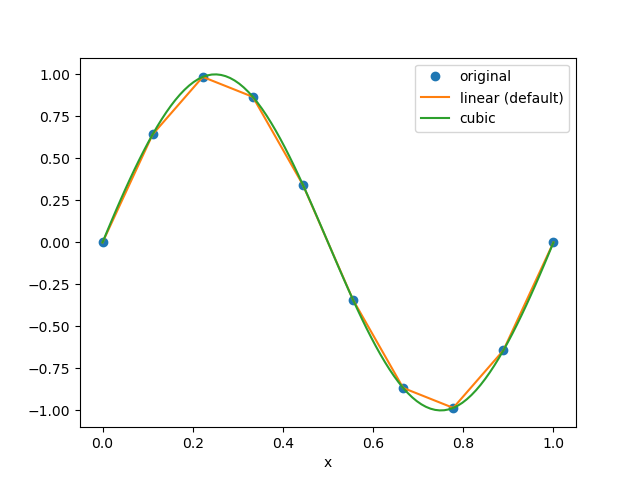
In [16]: da = xr.DataArray(np.sin(np.linspace(0, 2 * np.pi, 10)), dims='x',
....: coords={'x': np.linspace(0, 1, 10)})
....:
In [17]: da.plot.line('o', label='original')
Out[17]: [<matplotlib.lines.Line2D at 0x7f5b9444f2e8>]
In [18]: da.interp(x=np.linspace(0, 1, 100)).plot.line(label='linear (default)')
�������������������������������������������������������Out[18]: [<matplotlib.lines.Line2D at 0x7f5bd7ac3320>]
In [19]: da.interp(x=np.linspace(0, 1, 100), method='cubic').plot.line(label='cubic')
��������������������������������������������������������������������������������������������������������������Out[19]: [<matplotlib.lines.Line2D at 0x7f5bd7b881d0>]
In [20]: plt.legend()
���������������������������������������������������������������������������������������������������������������������������������������������������������������������Out[20]: <matplotlib.legend.Legend at 0x7f5b945c8940>
Additional keyword arguments can be passed to scipy’s functions.
# fill 0 for the outside of the original coordinates.
In [21]: da.interp(x=np.linspace(-0.5, 1.5, 10), kwargs={'fill_value': 0.0})
Out[21]:
<xarray.DataArray (x: 10)>
array([ 0. , 0. , 0. , 0.813798, 0.604023, -0.604023,
-0.813798, 0. , 0. , 0. ])
Coordinates:
* x (x) float64 -0.5 -0.2778 -0.05556 0.1667 ... 0.8333 1.056 1.278 1.5
# extrapolation
In [22]: da.interp(x=np.linspace(-0.5, 1.5, 10), kwargs={'fill_value': 'extrapolate'})
����������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������Out[22]:
<xarray.DataArray (x: 10)>
array([-2.892544, -1.606969, -0.321394, 0.813798, 0.604023, -0.604023,
-0.813798, 0.321394, 1.606969, 2.892544])
Coordinates:
* x (x) float64 -0.5 -0.2778 -0.05556 0.1667 ... 0.8333 1.056 1.278 1.5
Advanced Interpolation¶
interp() accepts DataArray
as similar to sel(), which enables us more advanced interpolation.
Based on the dimension of the new coordinate passed to interp(), the dimension of the result are determined.
For example, if you want to interpolate a two dimensional array along a particular dimension, as illustrated below,
you can pass two 1-dimensional DataArray s with
a common dimension as new coordinate.
For example:
In [23]: da = xr.DataArray(np.sin(0.3 * np.arange(20).reshape(5, 4)),
....: [('x', np.arange(5)),
....: ('y', [0.1, 0.2, 0.3, 0.4])])
....:
# advanced indexing
In [24]: x = xr.DataArray([0, 2, 4], dims='z')
In [25]: y = xr.DataArray([0.1, 0.2, 0.3], dims='z')
In [26]: da.sel(x=x, y=y)
Out[26]:
<xarray.DataArray (z: 3)>
array([ 0. , 0.42738 , -0.772764])
Coordinates:
x (z) int64 0 2 4
y (z) float64 0.1 0.2 0.3
Dimensions without coordinates: z
# advanced interpolation
In [27]: x = xr.DataArray([0.5, 1.5, 2.5], dims='z')
In [28]: y = xr.DataArray([0.15, 0.25, 0.35], dims='z')
In [29]: da.interp(x=x, y=y)
Out[29]:
<xarray.DataArray (z: 3)>
array([ 0.556264, 0.634961, -0.466433])
Coordinates:
x (z) float64 0.5 1.5 2.5
y (z) float64 0.15 0.25 0.35
Dimensions without coordinates: z
where values on the original coordinates
(x, y) = ((0.5, 0.15), (1.5, 0.25), (2.5, 0.35)) are obtained by the
2-dimensional interpolation and mapped along a new dimension z.
If you want to add a coordinate to the new dimension z, you can supply
DataArray s with a coordinate,
In [30]: x = xr.DataArray([0.5, 1.5, 2.5], dims='z', coords={'z': ['a', 'b','c']})
In [31]: y = xr.DataArray([0.15, 0.25, 0.35], dims='z',
....: coords={'z': ['a', 'b','c']})
....:
In [32]: da.interp(x=x, y=y)
Out[32]:
<xarray.DataArray (z: 3)>
array([ 0.556264, 0.634961, -0.466433])
Coordinates:
x (z) float64 0.5 1.5 2.5
y (z) float64 0.15 0.25 0.35
* z (z) <U1 'a' 'b' 'c'
For the details of the advanced indexing, see more advanced indexing.
Interpolating arrays with NaN¶
Our interp() works with arrays with NaN
the same way that
scipy.interpolate.interp1d and
scipy.interpolate.interpn do.
linear and nearest methods return arrays including NaN,
while other methods such as cubic or quadratic return all NaN arrays.
In [33]: da = xr.DataArray([0, 2, np.nan, 3, 3.25], dims='x',
....: coords={'x': range(5)})
....:
In [34]: da.interp(x=[0.5, 1.5, 2.5])
Out[34]:
<xarray.DataArray (x: 3)>
array([ 1., nan, nan])
Coordinates:
* x (x) float64 0.5 1.5 2.5
In [35]: da.interp(x=[0.5, 1.5, 2.5], method='cubic')
�������������������������������������������������������������������������������������������������������������Out[35]:
<xarray.DataArray (x: 3)>
array([nan, nan, nan])
Coordinates:
* x (x) float64 0.5 1.5 2.5
To avoid this, you can drop NaN by dropna(), and
then make the interpolation
In [36]: dropped = da.dropna('x')
In [37]: dropped
Out[37]:
<xarray.DataArray (x: 4)>
array([0. , 2. , 3. , 3.25])
Coordinates:
* x (x) int64 0 1 3 4
In [38]: dropped.interp(x=[0.5, 1.5, 2.5], method='cubic')
����������������������������������������������������������������������������������������������������������������Out[38]:
<xarray.DataArray (x: 3)>
array([1.190104, 2.507812, 2.929688])
Coordinates:
* x (x) float64 0.5 1.5 2.5
If NaNs are distributed randomly in your multidimensional array,
dropping all the columns containing more than one NaNs by
dropna() may lose a significant amount of information.
In such a case, you can fill NaN by interpolate_na(),
which is similar to pandas.Series.interpolate().
In [39]: filled = da.interpolate_na(dim='x')
In [40]: filled
Out[40]:
<xarray.DataArray (x: 5)>
array([0. , 2. , 2.5 , 3. , 3.25])
Coordinates:
* x (x) int64 0 1 2 3 4
This fills NaN by interpolating along the specified dimension. After filling NaNs, you can interpolate:
In [41]: filled.interp(x=[0.5, 1.5, 2.5], method='cubic')
Out[41]:
<xarray.DataArray (x: 3)>
array([1.308594, 2.316406, 2.738281])
Coordinates:
* x (x) float64 0.5 1.5 2.5
For the details of interpolate_na(),
see Missing values.
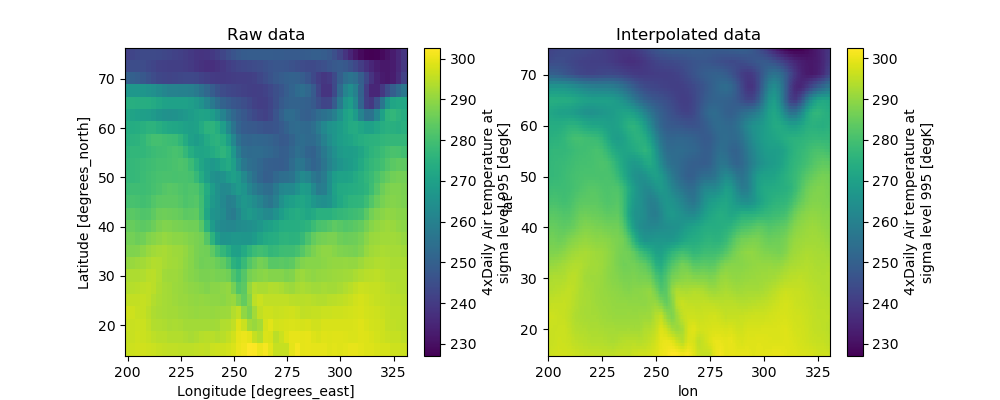
Example¶
Let’s see how interp() works on real data.
# Raw data
In [42]: ds = xr.tutorial.open_dataset('air_temperature').isel(time=0)
In [43]: fig, axes = plt.subplots(ncols=2, figsize=(10, 4))
In [44]: ds.air.plot(ax=axes[0])
Out[44]: <matplotlib.collections.QuadMesh at 0x7f5b94862278>
In [45]: axes[0].set_title('Raw data')
�������������������������������������������������������������Out[45]: Text(0.5, 1.0, 'Raw data')
# Interpolated data
In [46]: new_lon = np.linspace(ds.lon[0], ds.lon[-1], ds.dims['lon'] * 4)
In [47]: new_lat = np.linspace(ds.lat[0], ds.lat[-1], ds.dims['lat'] * 4)
In [48]: dsi = ds.interp(lat=new_lat, lon=new_lon)
In [49]: dsi.air.plot(ax=axes[1])
Out[49]: <matplotlib.collections.QuadMesh at 0x7f5b9489a128>
In [50]: axes[1].set_title('Interpolated data')
�������������������������������������������������������������Out[50]: Text(0.5, 1.0, 'Interpolated data')
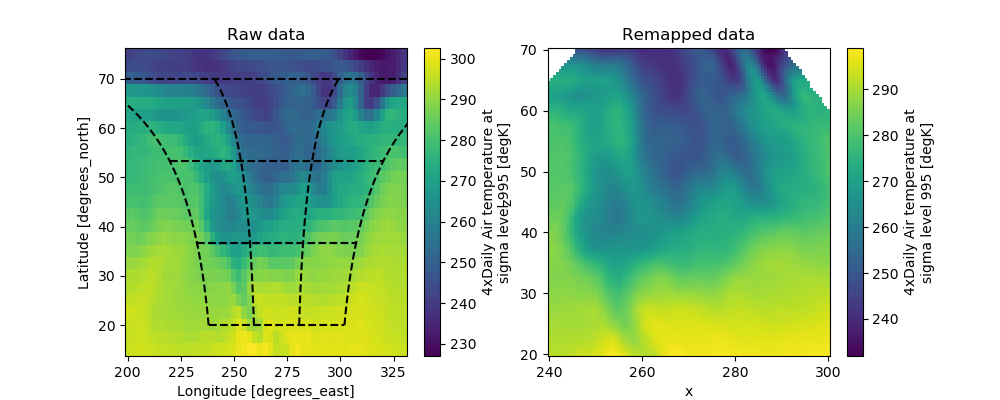
Our advanced interpolation can be used to remap the data to the new coordinate. Consider the new coordinates x and z on the two dimensional plane. The remapping can be done as follows
# new coordinate
In [51]: x = np.linspace(240, 300, 100)
In [52]: z = np.linspace(20, 70, 100)
# relation between new and original coordinates
In [53]: lat = xr.DataArray(z, dims=['z'], coords={'z': z})
In [54]: lon = xr.DataArray((x[:, np.newaxis]-270)/np.cos(z*np.pi/180)+270,
....: dims=['x', 'z'], coords={'x': x, 'z': z})
....:
In [55]: fig, axes = plt.subplots(ncols=2, figsize=(10, 4))
In [56]: ds.air.plot(ax=axes[0])
Out[56]: <matplotlib.collections.QuadMesh at 0x7f5b94449748>
# draw the new coordinate on the original coordinates.
In [57]: for idx in [0, 33, 66, 99]:
....: axes[0].plot(lon.isel(x=idx), lat, '--k')
....:
In [58]: for idx in [0, 33, 66, 99]:
....: axes[0].plot(*xr.broadcast(lon.isel(z=idx), lat.isel(z=idx)), '--k')
....:
In [59]: axes[0].set_title('Raw data')
Out[59]: Text(0.5, 1.0, 'Raw data')
In [60]: dsi = ds.interp(lon=lon, lat=lat)
In [61]: dsi.air.plot(ax=axes[1])
Out[61]: <matplotlib.collections.QuadMesh at 0x7f5bdcbb5320>
In [62]: axes[1].set_title('Remapped data')
�������������������������������������������������������������Out[62]: Text(0.5, 1.0, 'Remapped data')